Table of Contents

Anthropic 近期发布了一篇研究论文，旨在彻底回答在人工智能模型评估中，模型间性能差异是否仅仅是因为评估问题的选择而产生的随机性。文章通过引入统计理论和实验设计文献，结合 LLM 工作机制，提出了一系列建议（涉及到了中心极限定理、聚类标准误差、成对 t 检验和统计功效分析），以帮助研究人员以更加科学的方式报告评估（evals）结果。

像做社会科学实验一样评估实验对象——LLMs。

如果一个 AI 模型在基准测试中在测试常识或解决计算机编码问题的能力方面优于另一个模型，这种能力上的差异是否确实存在，还是该模型只是有幸在基准测试中选到了更有利于自己的问题？

为了更严谨地评估模型，成为了一个重要的议题。因为在构建AI系统时，企业无论是使用GPT、Claude、Gemini，还是采用开源的LLM，都会面临选择哪个模型最适合自己的问题。具体来说，哪个模型能更高效、更经济地解决自身业务问题？仅仅依赖MMLU等基准测试是不够的，因为这些测试未必能准确反映模型在实际生产环境中的表现。因此，理想的做法是开发团队能够动态收集真实业务系统中的问题，构建一个专属于自己的数据集，用于评估不同模型在特定场景下的实际表现。

而当团队需要进行模型评估时，Anthropic 的这篇 Blog 和相关论文提供了基于统计学方法的解决思路，能进一步推动模型在不同场景中的实际性能检测。

建议 1：使用中心极限定理

这条建议的核心是：利用中心极限定理，用标准误差来衡量模型评估的置信度。

模型评估通常基于大量不同的测试题，每个题目的得分存在随机性。简单的平均分并不能完全反映模型的真实能力，因为它受特定题目选择的影响。

中心极限定理指出，从同一分布中抽取多个样本，这些样本的平均值会近似服从正态分布。这个正态分布的标准差，被称为标准误差（SEM），可以用来衡量评估结果的可靠性。

NOTE

中心极限定理需要注意的几个关键点：

独立性要求：样本之间必须相互独立。这在实际应用中需要特别注意抽样方式。
同分布要求：所有样本都必须来自同一个分布。这意味着抽样条件应该保持一致。
样本量的影响：样本量越大，近似效果越好。这可以从上面的可视化中直观地看出。
标准误差：样本均值的标准差 (标准误差) 会随着样本量的增加而减小，其计算公式为 $\frac{\sigma}{\sqrt n}$ 。

例子1：
假设我们在测量一批苹果的重量。每个苹果的重量可能呈现任何分布 (比如偏重的多一些或者轻的多一些)。如果我们：

每次随机抽取 30 个苹果（这是一组样本）计算这 30 个苹果的平均重量（这是一个样本均值）重复这个过程 100 次（得到 100 个样本均值）这 100 个样本均值的分布就会近似正态分布，而且这个正态分布的：

均值会接近总体真实的平均重量（μ）标准差等于总体标准差除以样本容量的平方根（σ/√n）

例子2：
假设您想估计某个工厂生产的零件的平均长度。您随机抽取了多个样本，每个样本包含多个零件，并计算每个样本的平均长度。根据中心极限定理，随着样本数量的增加，这些样本平均长度的分布将近似于正态分布。这样，您可以利用这些样本均值来估计整个生产过程中零件的真实平均长度，并且可以计算出估计的置信区间，了解估计的准确性。

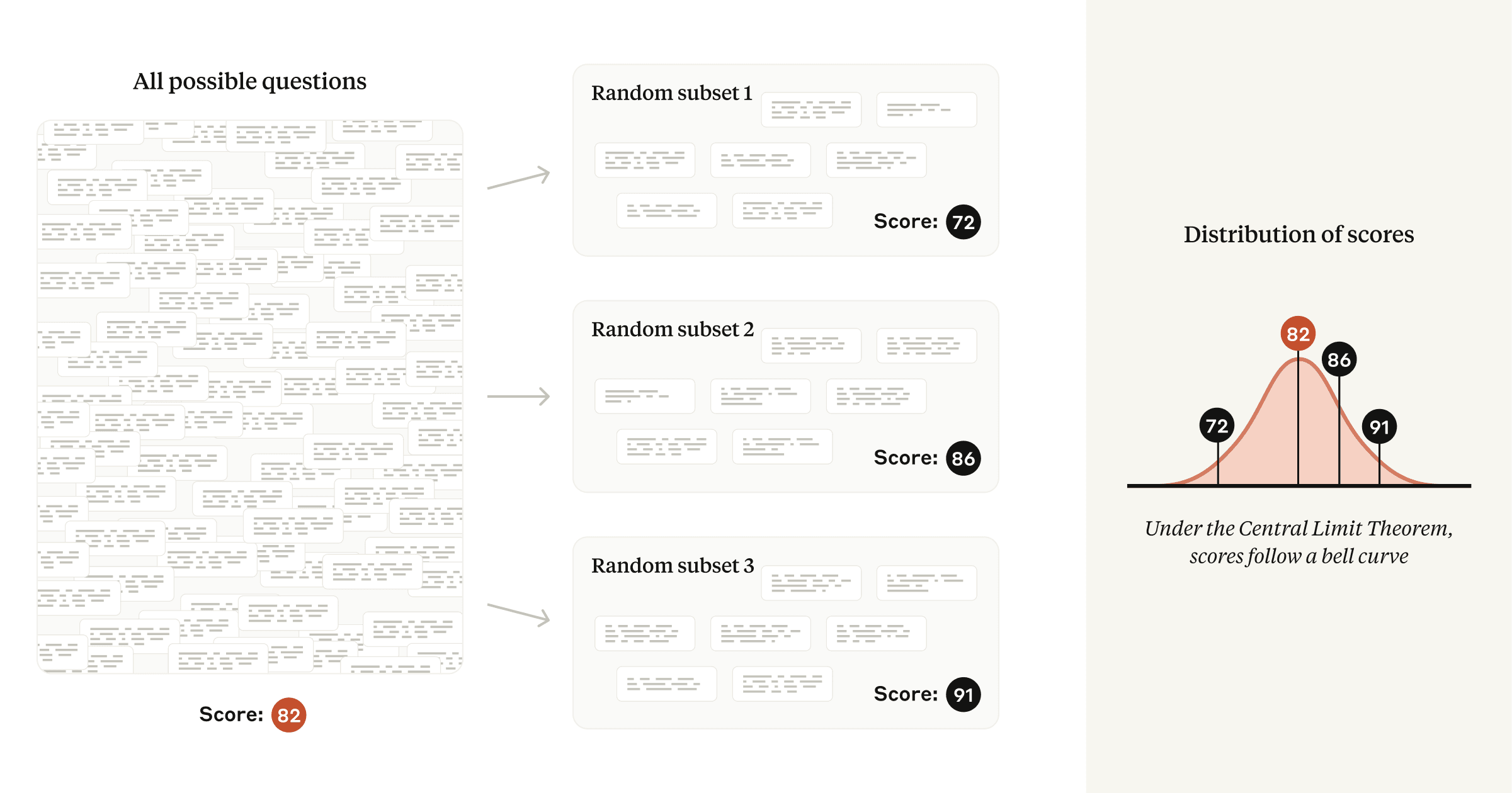如果我们想象评估问题是从一个“问题宇宙”中抽取的，那么评估分数将倾向于遵循正态分布，围绕所有可能问题的平均分数为中心。

因此，建议在报告模型评估分数时，不仅要给出平均分，还要给出标准误差。通过计算95%置信区间（平均分 ± 1.96 × SEM），可以更准确地估计模型在所有可能题目上的理论平均得分，从而更科学地评估模型的真实能力，避免被个别题目的随机性误导。

在论文中，中心极限定理（Central Limit Theorem, C.L.T.）用于计算评估得分均值的标准误差（Standard Error, SE）。具体的计算公式如下：

对于一个包含 (n) 个独立抽取的问题的评估，假设每个问题的得分为 ( $s_i$ )，那么评估得分的均值 ( $\hat {\mu}$ ) 可以估计为所有问题得分的平均值：

\hat{\mu} = \overline{s} = \frac{1}{n} \sum_{i=1}^{n} s_i

根据中心极限定理，评估得分均值的标准误差 ( $SE_{C.L.T.}$ ) 可以通过评估得分的样本方差 ( $\hat {\sigma}^2$ ) 来估计：

SE_{C.L.T.} = \sqrt{\frac{\hat{\sigma}^2}{n}}

其中，样本方差 ( $\hat {\sigma}^2$ ) 的计算公式为：

\hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^{n} (s_i - \overline{s})^2

将样本方差代入标准误差的公式，我们得到：

SE_{C.L.T.} = \sqrt{\frac{\frac{1}{n-1} \sum_{i=1}^{n} (s_i - \overline{s})^2}{n}}

简化后得到标准误差的最终计算公式为：

SE_{C.L.T.} = \sqrt{\frac{1}{n(n-1)} \sum_{i=1}^{n} (s_i - \overline{s})^2}

这个公式用于估计评估得分均值的标准误差，它量化了由于样本限制而产生的不确定性。在报告评估结果时，这个标准误差通常与均值一起报告，以便更好地理解和比较评估结果的统计显著性。

建议 2：聚类标准误差

这条建议的核心是：当评估题目存在关联性时，需要使用聚类标准误差，避免低估评估结果的不确定性。

当问题是以簇的形式抽取时，中心极限定理的一个关键假设 —— 即抽取的问题是相互独立的 —— 就被违反了。因此，直接使用中心极限定理计算的标准误差会导致不准确的结果，通常是低估了实际的方差。

WARNING

很多评估中，题目并非完全独立，而是存在关联性，例如阅读理解评估（如 DROP、QuAC、RACE 和 SQuAD）以及多语言评估（如 MGSM）中，多个题目可能基于同一段文本，这种情况下，简单地应用中心极限定理会低估标准误差，导致对模型能力差异的误判，因为来自同一段文本或类似来源的题目提供的信息量小于相同数量的独立题目。

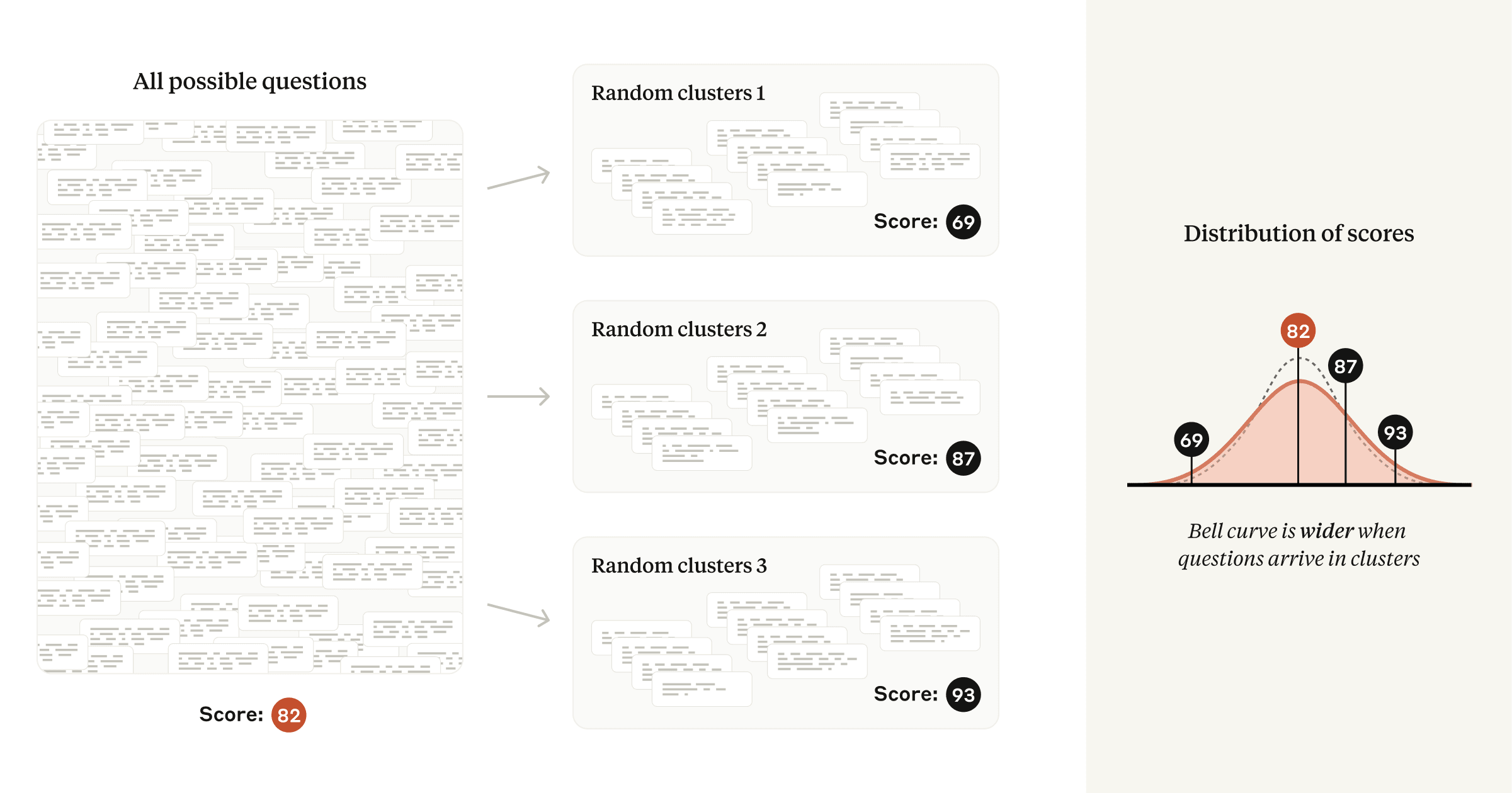如果问题出现在相关簇中——阅读理解评估中的常见模式——评估分数将比非簇状情况更加分散。

为了解决这个问题，需要使用聚类标准误差。具体来说，需要根据题目的关联性进行分组（例如，基于同一段文本的题目分为一组），然后在计算标准误差时考虑组内题目的相关性。

实际应用中，聚类标准误差往往比简单计算的标准误差大得多，有时甚至能达到三倍以上。忽略题目的关联性，使用简单的标准误差，可能会误以为模型之间存在显著差异，而实际上这种差异并不存在。因此，在存在题目关联性的评估中，使用聚类标准误差至关重要，可以更准确地评估模型能力的差异。

论文提供了计算聚类标准误差的公式，该公式考虑了问题之间在同一簇内的相关性。具体来说，如果 ( $s_{i,c}$ ) 表示簇 ( c ) 中第 ( i ) 个问题的得分，那么聚类标准误差 ( $SE_{clustered}$ ) 的计算公式为：

SE_{clustered} = \sqrt{SE_{C.L.T.}^2 + \frac{1}{n^2} \sum_{c} \sum_{i} \sum_{j \neq i} (s_{i,c} - \overline{s})(s_{j,c} - \overline{s})}

建议 3：减少问题内部的差异

这条建议的核心是：通过减少单个题目得分中的方差，可以提高整体评估结果的精确度。

模型在单个题目上的得分可以分解为两部分：平均得分（模型多次回答同一问题后的平均得分）和随机成分（实际得分与平均得分之间的差异）。根据总方差定律，减少随机成分的方差可以直接降低整体平均分的标准误差，从而提高统计精度。

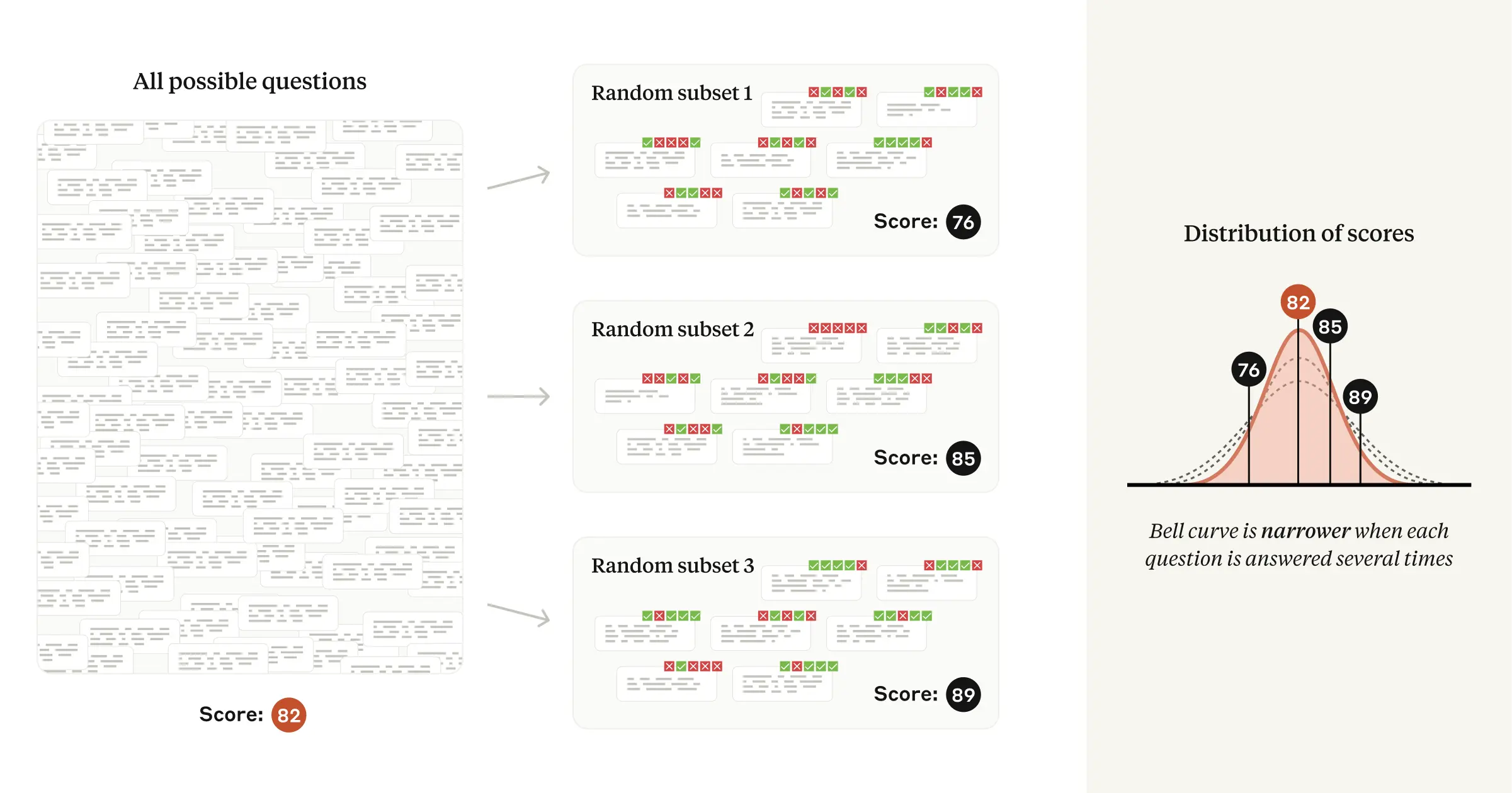如果模型是非确定性地生成答案，那么每道题生成（和评分）多个答案将导致评价分数不那么分散。

IMPORTANT

文章提出了两种减少随机成分方差的策略，取决于是否使用思维链（CoT）提示：

使用思维链提示时： 建议多次采样模型对同一题目的回答，并使用这些回答的平均得分作为该题目的得分。这相当于对同一题目进行多次“测试”，然后取平均值，从而减少随机性的影响。
不使用思维链提示时： 建议使用语言模型的下一个词元概率作为题目得分。例如，对于多项选择题，可以直接使用模型预测正确答案的概率作为得分。这种方法可以完全消除随机成分，因为模型的输出是概率分布，而不是单一的答案。例如，如果多选题的正确答案是 "B"，我们只需使用模型生成标记 "B "的概率作为问题得分。

通过这两种方法，可以有效降低单个题目得分中的方差，从而提高整体评估结果的精确度，使我们对模型能力的评估更可靠。

建议 4：分析配对差异

评估分数本身没有任何意义；它们只有在相互关系中才有意义（一个模型优于另一个模型，或追平另一个模型，或优于某个人）。但是，两个模型之间的测量差异会不会是由于评估中特定问题的选择以及模型答案的随机性造成的呢？我们可以通过双样本 t 检验来找出答案，只需使用从两个评估得分中计算出的平均值的标准误差即可。

这种方法的核心在于，对于每个问题，同时使用所有模型进行评估，并分析每个模型对同一问题的得分差异。这种配对比较减少了由于问题之间变异性引起的噪声，使得模型性能差异的评估更加精确。此外，配对差异分析能够考虑到模型得分之间可能存在的相关性，这对于评估模型的相对表现至关重要。通过这种方法，研究人员可以更有信心地断言模型性能的改进是否真实存在，并且能够更准确地量化这些改进。

在实践中，论文发现不同的前沿模型在流行 evals 中的问题得分有很大的相关性--在-1 到+1 的范围内，相关性在 0.3 到 0.7 之间。换句话说，前沿模型总体上倾向于把相同的问题做对或做错。因此，配对差分分析是一种 "免费 "的方差缩小技术，非常适合人工智能模型评估。因此，为了从数据中提取最清晰的信号，论文建议在比较两个或多个模型时，报告配对信息--均值差异、标准误差、置信区间和相关性。

未配对分析

未配对分析提供了一种方法来评估和比较两个模型的性能，即使它们可能是在不同的问题集上评估的。通过这种方式，研究人员可以确定一个模型是否在统计上优于另一个模型，即使它们没有在完全相同的条件下进行评估。

对于未配对分析（Unpaired analysis），即比较两个模型 A 和 B 在评估得分上的差异时，计算常见的 95% 置信区间和 z-score 的方法如下：

计算两个模型得分的差异：首先计算两个模型的平均评估得分之差，记为： $\hat {\mu}_{A-B} = \hat {\mu}_{A} - \hat {\mu}_{b}$
计算差异的标准误差：接着计算这个差异的标准误差 ( $SE_{A-B}$ )，它是两个模型标准误差的平方和的平方根，其中 ( $SE_{A}$ ) 和 ( $SE_{B}$ ) 分别是模型 A 和 B 的标准误差。 $SE_{A-B} = \sqrt{SE_{A}^2 + SE_{B}^2}$
计算 95% 置信区间：使用 z 分布的 95% 置信区间的 z 值（通常为 1.96），计算置信区间： $CI_{A-B, 95\%} = \hat{\mu}_{A-B} \pm 1.96 \times SE_{A-B}$
计算 z-score：z-score 是衡量差异与标准误差之间关系的统计量，计算公式为： $z_{A-B} = \frac{\hat{\mu}_{A-B}}{SE_{A-B}}$ 这个值可以用来判断差异是否具有统计学意义。如果 z-score 的绝对值大于或等于 1.96，则表明在 95% 的置信水平下，两个模型之间存在显著差异。

配对分析

当两个模型评估同一组问题时，令 $s_{A-B,i} = s_{A,i} - s_{B,i}$ 表示第 $i$ 个问题上的分数差异，令 $\bar{s}_{A-B} = \bar{s}_A - \bar{s}_B$ 表示观测到的平均差异，我们可以估算出估计差值的标准误差为：

\mathrm{SE}_{A-B,\text{paired}} = \sqrt{\mathrm{Var}(s_{A-B}) / n} = \sqrt{\left( \frac{1}{n-1} \sum_i \left( s_{A-B,i} - \bar{s}_{A-B} \right)^2 \right) / n}

利用上述配对分析的公式，可以根据 $\mathrm{SE}_{A-B,\text{paired}}$ 计算出对应的置信区间与 z 分数。

如下面的例子，论文建议报告时将成对差异、标准误差、置信区间和相关性值作为主要结果的补充呈现。在上面的虚构数据中，两个模型（Galleon 与 Dreadnought）在 MATH 上的差异在统计上显著（置信区间为正），但在 HumanEval 和 MGSM 上的差异在 5%的水平上并不显著。

Eval	Model	Baseline	Model - Baseline	95% Conf. Interval	Correlation
MATH	Galleon	Dreadnought	+2.5% (0.7%)	(+1.2%, +3.8%)	0.50
HumanEval	Galleon	Dreadnought	-3.1% (2.1%)	(-7.2%, +1.0%)	0.64
MGSM	Galleon	Dreadnought	-2.7% (1.7%)	(-6.1%, +0.7%)	0.37

因此，只要模型分数的条件均值存在相关性，我们就可以通过配对差异来减小方差；也就是说，如果两个模型在判断哪些问题“简单”以及哪些问题“困难”上存在一定程度的一致性。

在论文中，作者展示了配对差异检验的结果将如何与两个模型问题得分之间的皮尔逊相关系数相关联。相关系数越大，平均差的标准误差就越小。

标准误差的聚类版本，适用于 DROP、QuAC、RACE、SQuAD、MGSM 以及其他相关组中抽取问题的评估，可以直接从差异中计算得出：

\mathrm{SE}_{A-B,\text{paired,clustered}} = \sqrt {\frac{1}{n} \left( \sum_c \sum_i \sum_j (s_{A-B,i,c} - \bar{s}_{A-B})(s_{A-B,j,c} - \bar{s}_{A-B}) \right)}

建议 5 ：使用功效分析

从统计学家的角度来看，统计功效（statistical power）是统计检验中与统计显著性（statistical significance）相对的概念。统计功效指的是，当两个模型之间确实存在差异时，统计检验能够正确检出差异的能力。

如果评估中包含的问题数量较少，与任何统计检验相关的置信区间（confidence interval）通常会比较宽。置信区间较宽的结果是，模型之间需要存在较大的实际差异，才能在统计上被识别为显著差异。而对于较小的差异，可能会由于样本量不足或变异性过大，无法被检测到。

功效分析（power analysis）研究的是以下几个因素之间的数学关系：

观测数量（sample size），即实验中包含的样本或观测的数量；
统计功效（power），即检测到真实差异的概率；
假阳性率（false positive rate, α），即当实际上没有差异时，错误地得出有显著差异的概率；
效应量（effect size），即我们希望检测到的差异的实际大小。

功效分析的目标通常是确定所需的样本量，以便在给定的效应量和显著性水平（通常为 0.05）下，确保足够的功效（通常为 0.8 或 80%）。在实际中，小样本量会导致功效不足，这意味着可能会错过小的、但有实际意义的模型改进。

IMPORTANT

论文中展示了如何将功率分析的概念应用于评估。具体来说，向研究人员展示了如何提出一个假设（如模型 A 比模型 B 高出 3 个百分点），并计算出为了检验这个假设与零假设（如模型 A 和模型 B 打成平手）之间的差异，评估应包含的问题数量。

样本量公式描述了两个模型之间的假设差异与实验中问题数量之间的关系，它应该在几个方面被证明是有用的。现有评估的用户可以使用该公式来确定从一个大型评估中抽取的问题数，样本量计算公式的输入包括：

显著性水平 α，表示零假设下的 I 类错误率；
功率水平 1-β，其中 β 表示备择假设下的 II 类错误率；
最小可检测效应 δ，表示备择假设下两个模型之间的平均得分差异。 $\begin{align} \omega^2 &= \operatorname{Var}(x_A) + \operatorname{Var}(x_B) - 2 \operatorname{Cov}(x_A, x_B) \\ \sigma_A^2 &= \mathbb{E}[\sigma_{A,i}^2] \\ \sigma_B^2 &= \mathbb{E}[\sigma_{B,i}^2] \end{align}$ 让 zp 代表标准正态分布的 (1 - p)th 百分位数。我们假设进行上述的配对分析，答案将从模型 A 中抽样 KA 次，从模型 B 中抽样 KB 次（在最简单的情况下，KA = KB = 1）。那么，在给定最小可检测效应 δ 的情况下，要达到 I 类错误率 α 和 II 类错误率 β 所需的独立问题数 n 为： $n = \frac{(z_{\alpha/2} + z_{\beta})^2 \left( \omega^2 + \frac{\sigma_A^2}{K_A} + \frac{\sigma_B^2}{K_B} \right)}{\delta^2}$

结语

统计学是在噪声存在的情况下进行测量的科学。评估（Evals）存在许多实际挑战，真正意义上的评估科学尚未成熟。统计学只能构成评估科学的一个方面，但却是至关重要的一部分，因为任何一门实证科学的可靠性都取决于其测量工具的精度。

本文参考自 Anthropic 的研究论文： https://arxiv.org/abs/2411.00640 ，更多本文未提及的计算公式可查阅该论文，都有详细的公式描述，实践中可以根据需要应用于模型评估。

欢迎关注微信公众号👏 code

欢迎微信扫码加入我的付费知识星球👏 code