• L1正则化与L2正则化 - 知乎
• l1 相比于 l2 为什么容易获得稀疏解？ - 知乎

概念

L1正则化（也称为 Lasso 正则化）添加的是权重绝对值的和，而 L2正则化（也称为 Ridge 正则化）添加的是权重平方的和。这些正则化方法对权重的影响不同：

• L1正则化倾向于产生更多的零权重或稀疏权重矩阵，从而实现特征选择。
• L2正则化则倾向于分散权重到所有特征上，使得权重值更小、更平均。

L1 和 L2 正则化之所以这样命名，是因为它们与数学中的范数概念有关。范数是一个函数，用于给定向量空间中的向量分配一个非负长度或大小。在不同的上下文中，范数可以用于衡量向量的长度或复杂度。

• L1 范数：也称为“曼哈顿范数”或“一范数”，是向量中各元素绝对值之和。对于向量 $v = [v_1, v_2, ..., v_n]$，L 1 范数定义为 $\|v\|_1 = \sum_{i=1}^{n} |v_i|$。在机器学习中，L 1 范数用作正则化项时，它会倾向于产生稀疏的权重向量，因为它对于小的非零权重施加了较大的惩罚，这可能导致权重值归零。
• L 2 范数：也称为“欧几里得范数”或“二范数”，是向量中各元素平方和的平方根。对于向量 v ，L 2 范数定义为 $||v||_2 = \sqrt{\sum_{i=1}^{n} v_i^2}$。在机器学习中，当 L 2 范数用作正则化项时，它会倾向于让所有权重都趋近于零，但不会完全为零，这有助于处理过拟合问题，同时保持权重的值分布均匀。

在正则化的上下文中，L 1 正则化添加的是权重的 L 1 范数作为惩罚项，而 L 2 正则化添加的是权重的 L 2 范数平方作为惩罚项。这些范数帮助定义了在机器学习中如何衡量模型复杂性，并且它们的几何解释有助于我们理解它们在模型优化过程中的作用。

loss 函数图像

原损失函数等高线，越接近圆心表示越到全局最优点：

这个图像是关于机器学习中梯度下降优化算法的一个可视化。在这个上下文中，$W^1$ 和 $W^2$ 代表模型参数，它们可能是一个线性回归或神经网络模型中的权重。这张图显示了一个损失函数的等高线图，每一条彩色的曲线代表损失函数在不同的 $W^1$ 和 $W^2$ 值时的相同水平。

这里的关键点是理解等高线是损失函数的可视化，损失函数量化了模型预测值和实际值之间的差距。等高线越紧密，表明在那个区域损失函数的变化越剧烈。等高线的中心（通常是最内圈）代表了损失函数的最小值，也就是我们想通过优化算法找到的最优点。

在梯度下降算法中，我们从某个初始点（在图中用黑点表示）开始，计算损失函数关于参数的梯度（即斜率），然后在梯度的反方向上更新参数值，因为这个方向是损失最快减少的方向。通过迭代这个过程，我们希望能够达到最内圈，找到使损失函数最小化的参数值。在这个过程中，我们通过等高线的形状来了解参数空间内损失函数的地形。

在这个图中，梯度下降的路径可能看起来是曲折的，因为梯度的方向是直接指向最陡峭下降的方向，而不一定是指向最终最小值的最短路径。这也展示了优化过程可能会遇到的复杂性，特别是在参数空间的维度更高时。

加入 L1 与 L2

L1和L2加入后的函数图像：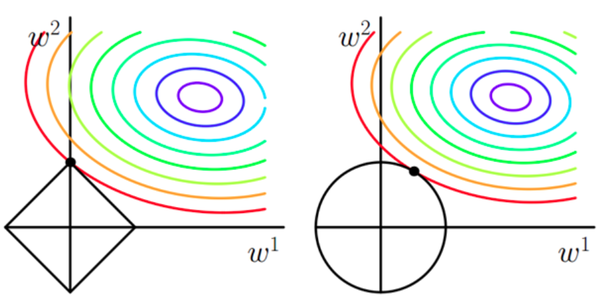

在机器学习中，L 1 和 L 2 是两种常见的正则化方法，它们被用来防止模型过拟合。正则化通过在损失函数中添加一个额外的项来工作，这个项惩罚模型复杂度，通常是模型权重的函数。

左边的图展示了 L 1 正则化的影响，也称为 Lasso 正则化。它通过向损失函数添加权重的绝对值之和来工作。在图像上，这对应于一个菱形区域。L 1 正则化倾向于产生稀疏的权重矩阵，即很多权重值会变成零。这可以通过等高线图中的菱形造成的“角”来理解，在这些角上，算法很容易找到使某些权重为零的解。

右边的图展示了 L 2 正则化的影响，也称为 Ridge 正则化。它通过向损失函数添加权重的平方和来工作。在图像上，这对应于一个圆形区域。L 2 正则化会惩罚权重的平方，因此它倾向于使权重均匀地小，而不是完全为零。

两张图中的黑色点表示开始优化的点，而曲线代表梯度下降的路径。在这两种情况下，梯度下降的路径会被正则化项影响。L 1 正则化可能导致路径沿着轴走，这是因为它倾向于产生具有零值的权重。相反，L 2 正则化的路径更加平滑，不会有突然的改变方向，因为它倾向于均匀地缩小权重的大小。

最终，这些正则化项的作用是影响梯度下降算法找到的权重解，通过惩罚大的权重值，它们帮助减少模型的过拟合，提高模型的泛化能力。

L1 为什么容易获得稀疏解

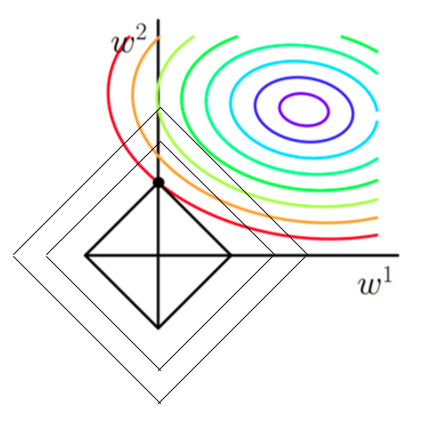
这张图是 L 1 正则化（Lasso 正则化）在参数优化中的可视化。在这个场景中，$W^1$ 和 $W^2$ 表示模型的两个参数，而彩色的等高线代表原始损失函数的值。原始损失函数可能是基于数据误差的，比如均方误差。

L 1 正则化向损失函数添加了一个与参数的绝对值成正比的项，这种正则化倾向于产生稀疏的参数向量，意味着许多参数会变为零。在图形表示中，L 1 正则化的效果是通过在原始损失函数上叠加一个以原点为中心的菱形轮廓来表示的。这个菱形轮廓代表了由于 L 1 正则化项导致的额外损失。

图中的黑色线代表梯度下降路径。梯度下降是一种优化算法，它试图找到损失函数的最小值。在未添加 L 1 正则化的情况下，梯度下降会直接朝向损失最小的中心点移动。但是，当加入 L 1 正则化后，优化路径会受到正则化项的影响，倾向于朝向参数值较小（甚至为零）的解。

在这张图中，可以看到，梯度下降的路径在接近菱形的顶点时会有所改变。这些点对应于其中一个参数为零的情况，这就是 L 1 正则化促使模型参数稀疏化的地方。优化路径通常会沿着菱形的边缘进行，这表明了在某个参数减少到零的同时另一个参数仍在被优化。

梯度下降的最终停止点可能位于菱形的顶点，这意味着其中一个参数会是零，从而产生了一个更简单的模型，这可能有助于防止过拟合，特别是当我们处理具有高维特征空间的数据集时。通过这种方式，L1正则化不仅有助于提高模型的泛化能力，还可以进行特征选择，通过将不重要的特征权重降为零。

欢迎关注微信公众号👏

欢迎微信扫码加入我的付费知识星球👏