Word2Vec

Word2Vec 是一类用于学习词向量的算法统称，由 Tomas Mikolov 等人在 2013 年引入。词向量是将词汇表中的词表示为数学上的向量，这些向量能够捕捉词之间的语义和句法关系。Word2Vec 通过训练神经网络模型来生成这样的词向量，而这些词向量非常适合用于各种自然语言处理任务。可以说，Word2Vec 构成了现在 LLM 的底层原理也不为过。

Word2Vec 模型在训练完成后，隐藏层的权重矩阵中的每一行，对应一个词的词向量。这些词向量具有捕捉语义和句法关系的能力。例如，向量算法可以揭示类似的关系，如 “king” - “man” + “woman” ≈ “queen”。

两种模型架构

Word2Vec 有两种基本的模型架构：Skip-Gram 和 Continuous Bag of Words (CBOW)。

1. Skip-Gram：目标是给定一个词来预测其上下文环境中的词。例如，输入一个句子: the quick brown fox jumps over the lazy dog，给定词 fox，模型试图预测在一个定义的窗口大小内 fox 前后的词，如 brown, jumps。一般经验 Skip-Gram 模型对于处理少见词较为有效，但是训练时长较长。
2. CBOW：与 Skip-Gram 相反，CBOW 的目标是使用某个词的上下文来预测这个词本身，由于上下文中单词的顺序并不重要，因此这种结构被称为词袋模型。CBOW 不具有顺序性，也不必具有概率性。例如，使用 the, brown, jumps, over 来预测 fox。CBOW 模型在小型数据集上表现更好，且训练速度比 Skip-Gram 快。通常情况下，CBOW 用于快速训练单词嵌入，这些嵌入用于初始化某些更复杂模型的嵌入。通常，这被称为预训练嵌入。

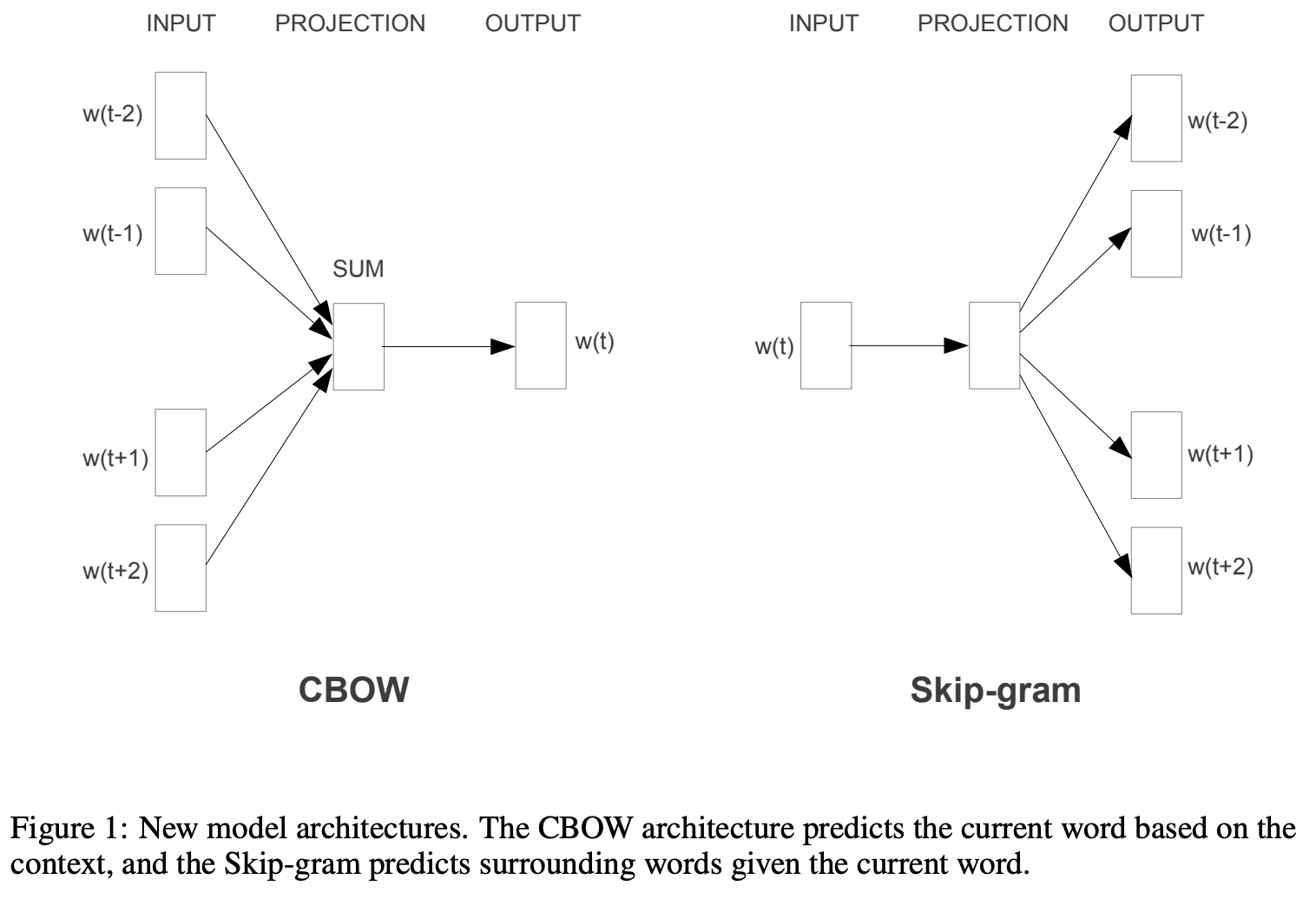
选择使用 Skip-gram 模型还是 CBOW 模型取决于你的需求。如果你的数据量较少或者出现生僻词，那么 Skip-gram 模型可能更适合，因为它能够更准确地生成词向量。但是，由于 Skip-gram 模型进行预测的次数要多于 CBOW，所以训练时间要比 CBOW 要长。如果你的数据量较大且没有太多生僻词，那么可以考虑使用 CBOW 模型，因为它训练速度快。

如何训练Skip-Gram模型

Skip-Gram 使用一个浅层的 3 层神经网络作为其基础架构：

• 输入层：对于 Skip-Gram，输入是目标词的 one-hot 编码。单词都由 one-hot 编码表示（比如说 the 这个单词排在所有单词前面，表示为[1, 0, 0, ... ]）， $V$ 个单词组成词汇表，所以 one-hot 编码的向量长度为 $V$；
• 隐藏层：没有激活函数的全连接层，将 one-hot 编码映射到隐藏层，这层实际上作为一个全连接的权重矩阵，这个矩阵就是词向量的查找表；
• 输出层：使用 softmax 函数，预测上下文（对于 Skip-Gram）或目标词（对于 CBOW）。

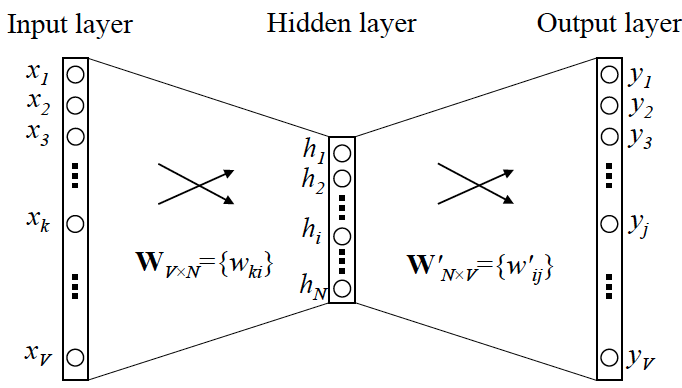
Word2Vec 的训练通常使用最大似然（通过 softmax）和负采样（一种优化的训练方式，只更新部分权重而非整个词汇表的权重）等技术。训练的目标是调整网络权重，以便模型输出的预测概率最大化实际观察到的词的概率。

下面我们将使用 pytorch 一步步搭建一个很简单的 Skip-Gram 神经网络模型，需要有 python 和 pytorch 的一些使用经验，以及一些深度学习的基础，没接触过的话可跳过，有兴趣的话建议看看，结合代码应该能较为清楚的讲明白。

构建训练数据

首先，我们先简单创造一些数据：

# 这里我们就用一句话当做我们的语料库就行了
data = ["the quick brown fox jumps over the lazy dog"]

接着我们需要将这条数据转为模型训练需要的形式：

# 设置上下文窗口大小
window_size = 2
# 创建训练数据（中心词和上下文词）
def create_dataset(text, window_size):
    words = text.split()
    word_pairs = []
    # 对每个单词，考虑前后的上下文窗口
    for i in range(len(words)):
        for w in range(-window_size, window_size + 1):
            context_idx = i + w
            if context_idx < 0 or context_idx >= len(words) or i == context_idx:
                continue
            word_pairs.append((words[i], words[context_idx]))
    return word_pairs

word_pairs = create_dataset(data[0], window_size)
print(word_pairs[:9])

create_dataset 这个函数通过滑动窗口方法创建词嵌入模型的训练数据。它遍历文本中的每个单词，将其与指定窗口范围内的上下文词配对，生成 (中心词, 上下文词) 的列表，上述代码将打印出 word_pairs 的前 9 个单词对：

[('the', 'quick'), ('the', 'brown'), ('quick', 'the'), ('quick', 'brown'), ('quick', 'fox'), ('brown', 'the'), ('brown', 'quick'), ('brown', 'fox'), ('brown', 'jumps')]

由于我们的 window_size=2，所以句子中的每个词，都会分别与其前后 2 个词一对一的组成一对，作为模型的一条训练数据，模型每次训练将会根据输入的 中心词 预测配对的 上下文词。

模型跑在计算机上，但是计算机是不认识字符串的，只知道数字，因此我们需要将每个单词用一个数字表示，相当于将单词编码成计算机认识的，后面模型输出数字后，再将其解码/映射回原本的单词：

# 创建词汇表和单词索引
def create_vocab(data):
    idx = 0
    word_to_idx = {}
    for sentence in data:
        for word in sentence.split():
            if word not in word_to_idx:
                word_to_idx[word] = idx
                idx += 1
    return word_to_idx

word_to_idx = create_vocab(data)
print(word_to_idx)

上述代码将打印出 word_to_idx 这个字典：

{'the': 0, 'quick': 1, 'brown': 2, 'fox': 3, 'jumps': 4, 'over': 5, 'lazy': 6, 'dog': 7}

之后我们搭建模型并完成训练后，这个字典中的每个单词对应的数字便是唯一的索引，我们可以根据这个索引找到一组向量，这个向量就是对应单词的词嵌入向量。

我们可以使用 word_to_idx 将 word_pairs 的单词对转为单词的索引对 idx_pairs：

idx_pairs = [(word_to_idx[word], word_to_idx[context]) for word, context in word_pairs]

print(idx_pairs[:9])

打印出来得到以下结果：

[(0, 1), (0, 2), (1, 0), (1, 2), (1, 3), (2, 0), (2, 1), (2, 3), (2, 4)]

搭建模型结构

前文提到输入模型训练的数据应该是单词 one-hot 编码后的，但是目前为止我们的代码没有把数据处理成 one-hot 编码后的样子，实际上在使用 pytorch 的时候，idx_pairs就可以作为训练数据直接输入接下来要搭建的模型了，因为 pytorch 会自动帮我们处理 one-hot 这一步。

在使用 pytorch 封装好的代码之前，我们先手动实现下论文中提到的将单词一个个 one-hot 后在送入模型训练的过程：

from torch import nn

size = 8 # 我们的 data 一共只有 8 个词
input = 3 # 对应构造数据中的 fox

def one_hot_encode(input, size):
       vec = torch.zeros(size).float()
       vec[input] = 1.0
       return vec

ohe = one_hot_encode(input, size)
linear_layer = nn.Linear(size, 1, bias=False)

# 随机为 8 个单词初始化 8 个嵌入向量
with torch.no_grad():
       linear_layer.weight = nn.Parameter(
              torch.rand(linear_layer.weight.shape)
)

print(f"fox one-hot 编码: {ohe}\n")
print(f"嵌入层权重: \n {linear_layer.weight}\n")
print(f"fox 嵌入向量: {linear_layer(ohe)}")

上述代码在我电脑上运行的结果如下：

fox one-hot 编码: tensor([0., 0., 0., 1., 0., 0., 0., 0.])

嵌入层权重:
 Parameter containing:
tensor([[0.0766, 0.4697, 0.1071, 0.4027, 0.9369, 0.5374, 0.3253, 0.6978]],
       requires_grad=True)

fox 嵌入向量: tensor([0.4027], grad_fn=<SqueezeBackward4>)

根据打印结果，我们一共为 8 个单词生成了 8 个范围在 0～1 的初始嵌入向量，其中索引为 3 的 fox 的 one-hot 编码为 tensor([0., 0., 0., 1., 0., 0., 0., 0.])，嵌入向量为 0.4027。

实际上我们的单词不会只有 8 个，而是几万几十万，每个单词的 one-hot 表示都相当稀疏；嵌入向量的维度一般也不会为 1，即只有一个维度的值，而是几百或上千个维度（比如 GPT 的嵌入向量为 2048/4096），且一般嵌入向量的维度越多，表征单词的能力就会越强，但是训练时长会越长。

因此，在 pytorch 中我们直接用 nn.Embedding 可以免去大量 one-hot 的麻烦，以及还有没提到自动求导计算梯度进行反向传播的过程。上述我们随机初始化的每个嵌入向量值都是需要在模型的训练中反复更新直到收敛的，我们可以看到调用 nn.Parameter 初始化嵌入向量打印出来的结果中有显示 requires_grad=True，该属性表示该张量需要计算梯度。这个属性有以下重要含义：

1. 梯度计算：PyTorch将会跟踪所有对该张量的操作，以便在反向传播时计算梯度。
2. 参与反向传播：训练模型时调用 loss.backward() 时，PyTorch会自动计算这个张量相对于损失的梯度。
3. 优化更新：这通常表明该张量是一个需要通过优化算法更新的模型参数。
4. 计算图构建：PyTorch会将这个张量纳入动态计算图中。
5. 内存使用：会占用额外内存来存储梯度信息。 这个属性常用于模型的可训练参数，如神经网络的权重和偏置。

以下例子供参考：

import torch
import torch.nn as nn

# 假设我们有一个小词汇表，大小为 100，每个词的嵌入维度为 10
embedding = nn.Embedding(100, 10)

# 假设我们想查找索引为 5 和 18 的词的嵌入
indices = torch.LongTensor([5, 18])
embeddings = embedding(indices)

print(embeddings)  # 输出将显示这两个词的 10 维向量

打印的结果：

tensor([[ 1.3747, -1.2362, -1.7319, -0.9151,  0.0768,  0.4594,  0.5592,  0.6832,
 -0.9756,  0.2924],
[ 0.3744,  0.4023, -0.3427, -1.3850, -1.4784,  0.9420,  1.2750, -0.3469,
  1.1398,  0.7630]], grad_fn=<EmbeddingBackward0>)

那么，接下来终于可以来搭建模型结构了：

import torch
import torch.nn as nn
import torch.nn.functional as F

# 模型定义
# 定义 Skip-Gram 神经网络模型（看训练数据可得）
class Word2Vec(nn.Module):
    def __init__(self, vocab_size, embedding_dim):
        super(Word2Vec, self).__init__()
        # 构建词嵌入lookup 表
        # 你可以将它想象为一个矩阵，其中行数等于词汇表的大小，列数等于嵌入的维度。
        self.embeddings = nn.Embedding(vocab_size, embedding_dim)
        self.linear = nn.Linear(embedding_dim, vocab_size)

    def forward(self, input_word_idx):
        embedded = self.embeddings(input_word_idx)
        output = self.linear(embedded)
        return output

模型很简单，就是一个 3 层的结构，输入层和中间的隐层（嵌入层）在 pytorch 中使用 nn.Embedding 即可完成，nn.Embedding 接收两个参数 vocab_size 和 embedding_dim，分别表示输入的词汇总数量（词汇表的大小，本质上就是因为输入层需要适配原始输入one-hot 编码向量的长度）和嵌入向量的维度（可以自己定）。 nn.Embedding 嵌入层本质上是一个线性层，其简化了我们上面手动实现 one-hot 编码向量输入与随机初始化嵌入向量的过程，最终存储一个可学习的查找表，表中的每一行对应一个词的嵌入向量。

nn.Embedding 之后接一个 nn. Linear 线性层作为输出层就可以了，输出层的输出向量维度为与 vocab_size 大小一样，因为我们要做的就是：输入某个单词的 one-hot 编码向量，从而预测其在训练数据中配对的上下文词，比如前面例子中的 ('quick', 'fox') 这一对，我们输入 quick 的 one-hot 向量（[0,1,0,0,0,0,0,0]），模型需要学习预测得到 fox 的 one-hot 向量（[0,0,0,1,0,0,0,0]），至于怎么学习的需要涉及到梯度下降、链式求导和反向传播等知识，pytorch 代码都设计封装好了，这里就不展开了。

最后，我们定义的模型 Word2Vec 还需要实现前向传播 forward 这个方法，从而定义输入的数据以怎样的顺序在神经网络的不同层间流动，流动时是怎么计算的。因为有了 nn. Embedding 自动帮我们处理 one-hot 与更新嵌入向量，所以这里我们定义好模型的输入层接收的数据为 input_word_idx 就好，也就是单词在词汇表中的索引（即 word_to_idx 字典存储的映射关系），最后的输出 output 是一个经过线性转换的嵌入向量。

训练模型

# 初始化模型和优化器
embedding_dim = 10
vocab_size = len(word_to_idx)
model = Word2Vec(vocab_size, embedding_dim)
optimizer = optim.SGD(model.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()

# 训练模型
def train(model, epochs):
    for epoch in range(epochs):
        total_loss = 0
        for center, context in word_pairs:
            center_idx = torch.tensor([word_to_idx[center]], dtype=torch.long)
            context_idx = torch.tensor([word_to_idx[context]], dtype=torch.long)
            optimizer.zero_grad()
            log_probs = model(center_idx)
            loss = criterion(log_probs, context_idx)
            # 启动反向传播
            loss.backward()
            # 更新模型的参数
            optimizer.step()
            total_loss += loss.item()
        print(f"Epoch {epoch + 1}/{epochs}, Loss: {total_loss/len(word_pairs)}")

# 训练模型
train(model, 50)

训练遵循以下 4 个步骤：

1. 选择优化器 optimizer（这里不展开讲）；
2. 选择损失函数，该任务可以被看作是一个多分类问题，即给定一个输入词，预测其上下文词的分布，那么一般选择 CrossEntropyLoss 作为损失函数；
3. 遍历训练数据集的所有数据 epochs 遍，计算并汇总损失 loss；
4. 根据计算得到的 loss 的梯度更新模型的参数。

先看下训练前 fox 随机初始化的嵌入向量：

print(model.embeddings.weight[word_to_idx["fox"]])

打印出：

tensor([-0.0607,  2.3524,  0.3049,  1.9660, -0.2083,  1.2522,  0.6136,  0.3793,
-0.3644,  0.8683], grad_fn=<SelectBackward0>)

训练后在打印一次：

tensor([ 1.9916, -0.4853, -0.3589, -0.1785,  0.9239,  0.5043, -0.0062,  0.0667,
0.6016, -0.0077], grad_fn=<SelectBackward0>)

可以看到，fox 的嵌入向量已经更新发生改变了。

在 Word2Vec 模型中，输出层通常是一个全连接层，它将隐藏层的输出（词向量）映射到一个新的向量，这个向量的维度与词汇表的大小相同。输出层的每个神经元都对应词汇表中的一个词，输出的值一般称作 logits，比如在我们这个例子中会得到一个 8 个值的 logits，那这个 logits 与要预测的 上下文词 有什么关系？例如要预测的是 dog，那么在我们的例子中其 one-hot 编码是 [0,0,0,0,0,0,0,1]，假如某次训练模型输出的 logits 是 [ 1.1838, 1.3771, 0.1656, 1.3511, 1.5058, -1.9800, -0.9093, -2.5280]。接下来，我们一般会用 softmax 函数用于将 logits 转换为一个概率分布。具体来说，每个 logit 会被转换成一个介于0和1之间的值，这些值加起来总和为1：

所以训练时，模型使用最大概率与实际的要预测的词的 one-hot 编码中的 1 的进行计算交叉熵损失¹来计算误差，并通过最小化交叉熵损失和反向传播来更新模型权重直到收敛。比如在上述预测 dog 的例子中，模型会不断通过更新权重让最后一位的 logits 转换成概率分布后的概率在跟其他 7 个 logits 相比时最大，这时候模型就能预测出 dog 了。

至此，我们用最简单的方式完成了 Skip-Gram 模型的搭建与训练，感谢阅读该部分，希望对你更好的理解 Word2Vec 有所帮助，有不对的地方也欢迎指正。至于 Skip-Gram 的其他实现方法和另一种 Word2Vec模型 CBOW 的实现，可以参考 pytorch 的官方 🔗 文档，可视化 Word2Vec 的可参考 🔗 链接。

Item2Vec

在 Word2vec 诞生之后，Embedding 的思想迅速从自然语言处理领域扩散到几乎所有机器学习领域，推荐系统也不例外。既然 Word2vec 可以对词“序列”中的词进行 Embedding，那么对于用户购买“序列”中的一个商品，用户观看“序列”中的一个电影，也应该存在相应的 Embedding 方法。

于是，微软于 2015 年提出了 Item2Vec 方法，它是对 Word2vec 方法的推广，使 Embedding 方法适用于几乎所有的序列数据。Item2Vec 模型的技术细节几乎和 Word2vec 完全一致，只要能够用序列数据的形式把我们要表达的对象表示出来，再把序列数据“喂”给 Word2vec 模型，我们就能够得到任意物品的 Embedding 了。

Item2vec 的提出对于推荐系统来说当然是至关重要的，因为它使得“万物皆 Embedding”成为了可能。对于推荐系统来说，Item2vec 可以利用物品的 Embedding 直接求得它们的相似性，或者作为重要的特征输入推荐模型进行训练，这些都有助于提升推荐系统的效果。

item2vec 原论文抛弃序列数据的时间信息，也就是说序列并不像文本一样，是有前后顺序表达的，并且在训练的过程中采用了负采样策略进行训练，有效提升了模型的训练效率。

Skip-gram with Negative Sampling

SGNS通过负采样策略有效地处理了数据的稀疏性，通过减少需要考虑的负样本数量，提高了训练效率。

SGNS 的核心思想是使用负采样策略来提高训练效率。
在传统的 Skip-Gram 模型中，为了预测一个目标单词的上下文单词，需要计算整个词汇表中所有单词的概率，这在计算上是非常昂贵的。而在 SGNS 中，负采样优化的目标是使正样本的概率尽可能高，而使负样本的概率尽可能低。这通过最大化正样本的联合概率和最小化负样本的联合概率来实现。对于每个正样本（即实际出现在上下文中的单词对），算法会随机选择几个负样本（即不出现在上下文中的单词），训练过程被转换为一个二分类问题，然后训练模型来区分正样本和负样本，只更新这些样本对应的模型参数。这样做大大减少了计算量，使得模型训练更加高效。

负采样策略的关键在于如何选择负样本。SGNS 通常使用一个简单的启发式方法，即根据单词的频率分布来选择负样本，较频繁的单词被选中的概率较高。这种方法基于一个事实，即高频单词更有可能出现在负样本中，而低频单词则更有可能是模型需要学习的有用信息。

在实践中，这种方法不仅适用于 NLP 领域，还可以扩展到推荐系统中的商品嵌入，其中商品代替单词，用户的购买或交互行为代替上下文。通过这种方式，SGNS 能够捕捉商品之间的相似性和关联性，为基于商品的协同过滤推荐系统提供支持。

pytorch 实现

class Item2VecDataset(Dataset):
    def __init__(self, interactions, window_size, vocab_size, num_negatives):
        self.data = []
        self.window_size = window_size
        self.vocab_size = vocab_size
        self.num_negatives = num_negatives
        for interaction in interactions:
            for i in range(len(interaction)):
                target = interaction[i]
                context = []
                for j in range(max(0, i - window_size), min(len(interaction), i + window_size + 1)):
                    if i != j:
                        context.append(interaction[j])
                for c in context:
                    self.data.append((target, c, context))

    def __len__(self):
        return len(self.data)

    def __getitem__(self, idx):
        target, context, all_context = self.data[idx]
        negatives = self.generate_negatives(all_context)
        return target, context, negatives

    def generate_negatives(self, context):
        negatives = []
        context_set = set(context)
        while len(negatives) < self.num_negatives:
            neg = random.randint(0, self.vocab_size - 1)
            if neg not in context_set:
                negatives.append(neg)
        return torch.tensor(negatives)

window_size = 3
vocab_size = len(gid_to_idx)
num_negatives = 5
# 准备数据
dataset = Item2VecDataset(indexed_interactions, window_size, vocab_size, num_negatives)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

查看训练数据的形式很重要，上述代码输入 Item2VecDataset 的数据类似如下，表示用户交互（点击或购买）过的物品序列，跟 Word2Vec 一样，物品都用一个唯一的 id 表示，在实际生产中，一般就用物品在数据库中的 id 表示就可以了。

[
	[0, 1, 2, 3, 4, 5, 6],
	[7, 8, 9, 10, 11, 12],
	[13, 14, 15, 16, 17],
	[18, 19, 20], [21, 22],
	[0, 22], [23, 24, 25, 26]
]

打印前 3 条 Item2VecDataset 构造的数据形式如下：

[
	(0, 1, [1, 2, 3]),
	(0, 2, [1, 2, 3]),
	(0, 3, [1, 2, 3])
]

每条数据是个 3 元组，分别表示（target, context, negatives）。

class Item2VecSkipGramModel(nn.Module):
	def __init__(self, vocab_size, embedding_dim):
	    super(Item2VecSkipGramModel, self).__init__()
	    self.target_embedding = nn.Embedding(vocab_size, embedding_dim)
	    self.context_embedding = nn.Embedding(vocab_size, embedding_dim)

	def forward(self, target, context, negatives):
	    target_embed = self.target_embedding(target)
	    context_embed = self.context_embedding(context)
	    neg_embed = self.target_embedding(negatives)

	    # 计算正样本得分
	    pos_score = torch.sum(target_embed * context_embed, dim=1)
	    # bmm计算一批负样本得分
	    neg_score = torch.bmm(neg_embed, target_embed.unsqueeze(2)).squeeze(2)

	    return pos_score, neg_score

	def get_embedding(self):
	    return self.target_embedding.weight.data

# 超参数设置
embedding_dim = 256
batch_size = 64
epochs = 3
learning_rate = 0.01

def train_model(model, dataloader, epochs, learning_rate, noise_ratio=1, device='cpu'):
	optimizer = optim.Adam(model.parameters(), lr=learning_rate)

	for epoch in range(epochs):
	    total_loss = 0
	    for target, context, negatives in dataloader:
	        target = target.to(device)
	        context = context.to(device)
	        negatives = negatives.to(device)

	        optimizer.zero_grad()
	        pos_score, neg_score = model(target, context, negatives)

	        # 计算正样本损失
	        pos_loss = -F.logsigmoid(pos_score).mean()
	        # 计算负样本损失
	        neg_loss = -F.logsigmoid(-neg_score).mean()
	        # 总损失
	        loss = pos_loss + noise_ratio * neg_loss

	        loss.backward()
	        optimizer.step()
	        total_loss += loss.item()

	    print(f"Epoch {epoch + 1}, Loss: {total_loss / len(dataloader)}")

训练结束后，类似于 Word2Vec，我们可以得到物品在我们数据中的嵌入向量Embedding，这对于推荐系统来说很有用，可以在获取不到用户和物品更多特征数据的情况下仅凭交互数据（当然交互数据不能太少）计算其相似性，从而完成推荐系统的推荐任务。

其实，嵌入 Embedding 并不是深度学习时代才有的，在传统机器学习模型应用于推荐系统的时代，Embedding 也被称为“隐向量”，它通过矩阵分解的方法为用户进行推荐。不过，使用深度学习强大的拟合能力，Embedding 会更精准，在深度学习浪潮中发挥着不可替代的作用。

万物皆可嵌入

嵌入 embedding 不仅仅只有 word2vec 与 item2vec，随着深度学习的发展，还有 Graph Embedding 图嵌入被提出，其利用类似知识图谱这样的图结构来构造数据，而不局限于序列数据，从而学习点与点之间更深层的关系，得到表征更精准的嵌入向量。

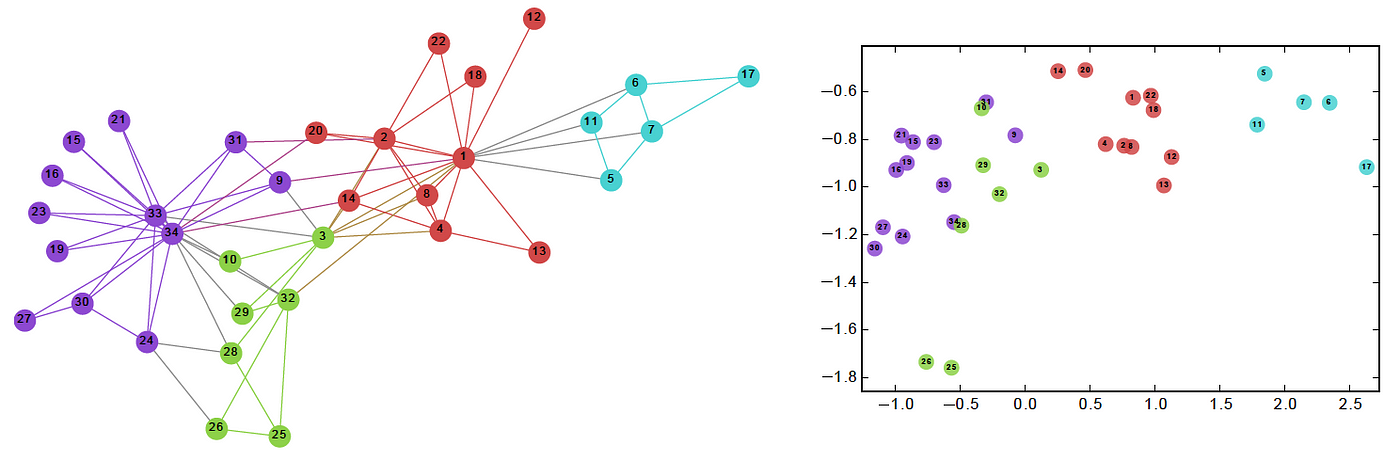
序列与图结构几乎可以表示世界上绝大多数事物间的联系，借由嵌入的方法，理论上万物皆可嵌入。现在嵌入在自然语言处理和推荐系统中也扮演者相当重要的角色，它们为这些领域带来了显著的进步和创新。

在自然语言处理中，词嵌入技术如 Word2Vec、GloVe 和 FastText 已经成为标准做法。这些方法将词语映射到连续向量空间，使得语义相近的词在这个空间中的距离也更近。这不仅提高了语言模型的性能，还为许多下游任务如情感分析、机器翻译等提供了强大的特征表示。随着 Transformer 架构的兴起，上下文化的嵌入方法（如 BERT、GPT 等）进一步推动了 NLP 的发展。这些模型能够根据词语在句子中的上下文动态生成嵌入，从而捕捉更细微的语义差异。

而推荐系统领域天然面对着大量稀疏的矩阵向量，嵌入技术的出现，使得物品和用户嵌入已经成为个性化推荐的核心技术。通过学习用户行为和物品特征的低维表示，推荐算法能够更准确地预测用户偏好，提供更加精准和多样化的推荐结果。像协同过滤、矩阵分解等传统方法都可以从嵌入的角度来理解和改进。

嵌入根据"物品"之间交互与联系，将离散稀疏的表示转化成连续稠密的表示，通过这种方法，我们将数据映射到另一个维度空间中，在那里挖掘数据的模式（pattern）与联系。这是一种强大的特征表征方式，但是我们难以对这些嵌入向量进行解释，因为它们缺乏直观的语义含义。

这种表示方法虽然在计算机处理和机器学习任务中表现出色，但对人类理解和分析造成了挑战。高维空间中的向量难以可视化，其中每个维度所代表的含义往往是抽象的，不能直接对应到原始数据的具体特征上。

此外，嵌入向量的生成过程通常是通过复杂的优化算法完成的，这使得我们难以追踪每个维度值是如何由原始数据推导出来的。这种"黑盒"特性在某些应用场景下可能会引发对模型可解释性和可信度的质疑。

尽管存在解释性的挑战，嵌入技术仍然是现代机器学习中不可或缺的工具。随着研究的深入，我们有望在保持其强大表现的同时，逐步提高其可解释性，从而在实际应用中获得更大的信任和更广泛的应用。

关于「认知」的三种观点

最后以深度学习之父 Geoffrey Hinton 教授关于「认知」的三种观点的采访内容作为本文的结束——

Hellermark：你认为人类大脑进化到能够很好地使用语言，还是语言进化到能够很好地与人类大脑配合？

Hinton：关于语言是否进化到与大脑配合，或者大脑是否进化到与语言配合的问题，我认为这是一个非常好的问题。我认为两者都发生了。

我曾经认为我们会在根本不需要语言的情况下进行很多认知活动，但现在我改变主意了。我举三种关于语言以及它与认知的关系的观点。

第一种，老式象征性观点，即认知由一些清理过的逻辑语言中的符号字符串组成，没有歧义，且应用推理规则。因此认知只是对像语言符号字符串这样的东西进行符号操作。这是一种极端观点。

另一种极端观点是：一旦进入大脑内部，一切都是向量。符号进来，你将这些符号转换为大型向量，所有的洞察都是用大型向量完成的。如果你想产生输出，你将再次产生符号。所以在 2014 年的机器翻译中有一个时刻，人们使用循环神经网络，单词会不断进来，它们会有一个隐藏状态，并在这个隐藏状态中不断累积信息。所以当到达句子的结尾时，就有一个大的隐藏向量，捕捉了句子的含义。然后它可以用来产生另一种语言中的单词，这被称为思维向量。这是关于语言的第二种观点。

还有第三种观点，也是我现在相信的，即大脑将这些符号转换为嵌入，并使用多层嵌入。所以你将得到非常丰富的嵌入。但嵌入仍然与符号相关联，从这个意义上讲，符号有其对应的大向量。这些向量相互作用产生下一个词的符号的向量。因此理解是指知道如何将符号转换为向量，以及向量的元素如何相互作用以预测下一个符号的向量。这就是大型语言模型以及我们的大脑中的理解方式。你保留符号，但将其解释为大向量。所有的工作以及所有的知识都在于使用哪些向量以及这些向量的元素如何相互作用，而不是在符号规则中。但这并不是说你完全摆脱了符号，而是说将符号转换为大向量，但保留符号的表面结构。这就是大型语言模型的运作方式。现在我认为这似乎也是人类思维一个更合理的模型。

参考

• Efficient Estimation of Word Representations in Vector Space
• Item2Vec Neural Item Embedding for Collaborative Filtering
• Implementing Word2Vec in PyTorch
• 可视化 word2vec
• Pytorch：How does nn.Embedding work?
• Hinton采访

欢迎关注微信公众号👏

欢迎微信扫码加入我的付费知识星球👏